El jurado ha destacado sus importantes aportaciones en el ámbito de las ecuaciones diferenciales parciales. En concreto, «por sus contribuciones fundamentales a la teoría de la regularidad de las ecuaciones no lineales en derivadas parciales, incluyendo los problemas de frontera libre y la ecuación de Monge-Ampèr».
Pocos matemáticos vivos han contribuido tanto a la comprensión de las ecuaciones diferenciales parciales como el argentino-estadounidense Luis Caffarelli / Academia Noruega de Ciencias y Letra
as ecuaciones diferenciales son herramientas que los científicos utilizan para predecir el comportamiento del mundo físico. Relacionan una o varias funciones desconocidas y sus derivadas, las cuales representan, respectivamente, magnitudes físicas y sus tasas de cambio. La ecuación diferencial define una relación entre ambas, desempeñando un papel destacado en muchas disciplinas, como la ingeniería, la física, la economía y la biología.
Las ecuaciones diferenciales parciales surgen de forma natural como leyes de la naturaleza, para describir fenómenos tan diferentes como el flujo del agua o el crecimiento de las poblaciones. Estas ecuaciones han sido fuente constante de intenso estudio desde los tiempos de Isaac Newton y Gottfried Leibniz. Sin embargo, a pesar de los considerables esfuerzos realizados por numerosos matemáticos a lo largo de los siglos, siguen sin resolverse cuestiones fundamentales de las soluciones en algunas ecuaciones clave.
Resultados técnicamente virtuosos
«Pocos matemáticos vivos han contribuido tanto a la comprensión de las ecuaciones diferenciales parciales como el argentino-estadounidense Luis Caffarelli, quien ha introducido técnicas nuevas e ingeniosas, ha demostrado una brillante perspicacia geométrica y ha producido muchos resultados fundamentales», ha destacado la Academia Noruega de Ciencias y Letras.
A lo largo de más de 40 años, Caffarelli ha realizado aportaciones revolucionarias a la teoría de la regularidad. La regularidad o ‘suavidad’ de las soluciones es esencial en los cálculos numéricos, y su ausencia es una medida de lo salvaje que puede comportarse la naturaleza.
«Los teoremas de Caffarelli han cambiado radicalmente nuestra comprensión de clases de ecuaciones diferenciales parciales no lineales con multitud de aplicaciones. Los resultados son técnicamente virtuosos y abarcan muchas áreas diferentes de las matemáticas y sus aplicaciones», afirma el presidente del Comité Abel, Helge Holden.
Los teoremas de Caffarelli han cambiado radicalmente nuestra comprensión de clases de ecuaciones diferenciales / Helge Holden, presidente del Comité Abel
Gran parte del trabajo del matemático se refiere a problemas de frontera libre. Por ejemplo, el problema de la fusión del hielo en el agua. En este caso, el límite libre es la interfaz entre el agua y el hielo, forma parte de la incógnita que hay que determinar. Otro caso es la filtración de agua a través de un medio poroso: también aquí hay que conocer la interfaz entre el agua y el medio.
Caffarelli ha dado soluciones a estos problemas con aplicaciones a interfaces sólido-líquido, flujos en chorro y de cavitación, de gas y líquido en medios porosos, así como a las matemáticas financieras.
Enorme impacto en el campo
«Combinando una brillante visión geométrica con ingeniosas herramientas y métodos analíticos, ha tenido y sigue teniendo un enorme impacto en este campo», afirma Holden.
El experto en ecuaciones diferenciales estudió Matemáticas en la Universidad de Buenos Aires, donde se doctoró en 1972. Un año después, se mudó a Minnesota (EE UU) para hacer un posgrado.
La carrera investigadora de este matemático argentino ha transcurrido en EE UU, y ha sido excepcionalmente prolífico, con más de 130 colaboradores y 30 estudiantes de doctorado
Desde entonces, su carrera investigadora ha transcurrido en universidades estadounidenses. Es un matemático excepcionalmente prolífico, con más de 130 colaboradores y más de 30 estudiantes de doctorado a lo largo de 50 años.
El catedrático de la Universidad de Texas ha recibido numerosos galardones, entre ellos el Leroy P. Steele Prize for Lifetime Achievement in Mathematics, y los Premios Wolf y Shaw.
El próximo 23 de mayo recibirá el Premio Abel en Oslo de manos del rey Harald de Noruega. Está financiado por el gobierno de ese país y su dotación es de 7,5 millones de coronas noruegas (676 500 euros).
El premio Abel lo concede anualmente la Academia Noruega de las Ciencias y las Letras a un investigador senior (a veces dos) como premio a toda su carrera. Es el mayor reconocimiento del campo de las matemáticas, junto a la Medalla Fields, que concede cada cuatro años la Unión Matemática Internacional, a un máximo de cuatro investigadores menores de 40 años.
Vinculación con España
Aunque reside y trabaja en EE UU, Caffarelli es miembro del Comité Externo de Asesoramiento Científico del ICMAT, el Instituto de Ciencias Matemáticas (un centro mixto del CSIC y las universidades Autónoma, Complutense y Carlos III de Madrid).
“La obra de Caffarelli, profunda y revolucionaria, ha resuelto una serie de problemas llamados de frontera libre”, explica Antonio Córdoba, catedrático emérito de la Universidad Autónoma de Madrid (UAM), miembro del ICMAT y colaborador de Caffarelli.
La obra de Caffarelli, profunda y revolucionaria, ha resuelto problemas llamados de frontera libre, como el que aparece al estudiar una mezcla de agua y hielo / Antonio Córdoba (ICMAT/UAM)
Cordaba también recuerda que un ejemplo de este problema aparece al estudiar una mezcla de agua y hielo: ¿cómo es la superficie de separación entre las dos fases sólido-líquido?, y otro es el denominado “problema del obstáculo”.
Imaginando una membrana elástica que se hace descender hasta tocar a un cuerpo apoyado en el interior de un recinto plano, al final del proceso la membrana queda pegada a los bordes del recinto. Habrá una zona de contacto en la que la membrana coincide con el obstáculo, mientras que fuera su forma debe satisfacer las ecuaciones de la elasticidad: ¿cómo es la curva frontera de la zona de contacto?
En casos como este, interesa estudiar cierta ecuación diferencial con unos datos fijos en los límites del espacio, pero esta frontera del dominio es desconocida y forma parte importante de la cuestión. “Hasta la aparición de los trabajos de Caffarelli en los años ochenta del pasado siglo solo se conocían resultados muy parciales. Pero Luis logró entender en profundidad estos problemas combinando métodos del análisis armónico con las ideas del cálculo de variaciones introducidas por Ennio de Giorgi y John Nash”, asegura Córdoba.
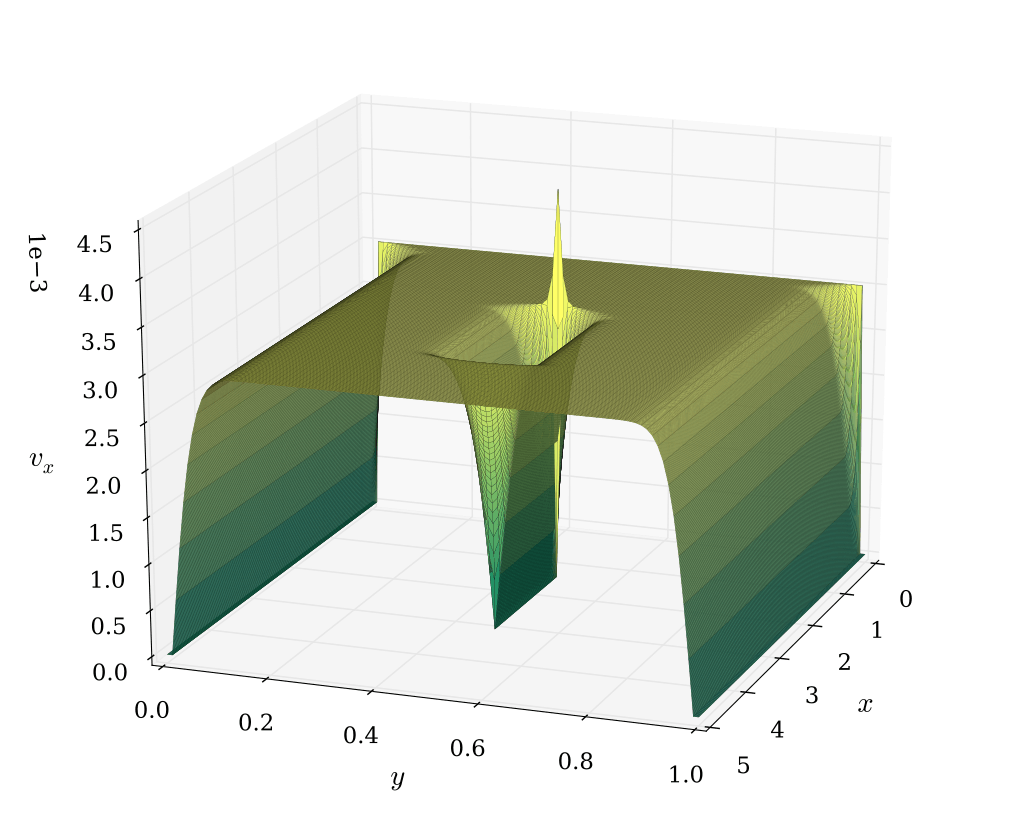
Ecuaciones diferenciales (de Navier-Stokes) utilizadas para simular el flujo de aire alrededor de una obstrucción. / IkamusumeFan
“Su intuición le permitió visualizar precisas estimaciones analíticas en términos geométricos y maleables”, afirma el matemático. Además, también resolvió otros problemas famosos que se habían resistido a varias generaciones de matemáticos, como las ecuaciones no-lineales de Monge-Ampère, o la naturaleza de transiciones de fase en los modelos de campo medio formulados por Ginzburg-Landau.
A mediados de la década de 1980 Caffarelli y Córdoba codirigieron un proyecto de investigación a través del cual organizaron diversas actividades como congresos y escuelas en la Universidad Internacional Menéndez Pelayo (UIMP) sobre ecuaciones en derivadas parciales.
Poco después, Caffarelli recibió el Doctorado Honoris Causa de la UAM. Su vinculación con esta universidad, y su colaboración con matemáticos españoles, ha sido muy intensa y fructífera. Pertenece, desde su fundación en 1985, al comité editorial de la Revista Matemática Iberoamericana.








